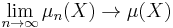Vitali–Hahn–Saks theorem
In mathematics, the Vitali–Hahn–Saks theorem (named for Giuseppe Vitali, Hans Hahn, and Stanisław Saks) states that given μn for each integer n >0, a countably additive function defined on a fixed sigma-algebra Σ, with values in a given Banach space B, such that
exists for every set X in Σ, then μ is also countably additive. In other words, the limit of a sequence of spectral measures is a spectral measure.